Control Bipedal Walker With PPO

import numpy as np
import scipy.signal
from gym.spaces import Box, Discrete
import gym
import time
import torch
import torch.nn as nn
from torch.optim import Adam
from torch.distributions.normal import Normal
from torch.distributions.categorical import Categorical

def combined_shape(length, shape=None):
    if shape is None:
        return (length,)
    return (length, shape) if np.isscalar(shape) else (length, *shape)


def mlp(sizes, activation, output_activation=nn.Identity):
    layers = []
    for j in range(len(sizes)-1):
        act = activation if j < len(sizes)-2 else output_activation
        layers += [nn.Linear(sizes[j], sizes[j+1]), act()]
    return nn.Sequential(*layers)


def count_vars(module):
    return sum([np.prod(p.shape) for p in module.parameters()])


def discount_cumsum(x, discount):
    """
    magic from rllab for computing discounted cumulative sums of vectors.
    input: 
        vector x, 
        [x0, 
         x1, 
         x2]
    output:
        [x0 + discount * x1 + discount^2 * x2,  
         x1 + discount * x2,
         x2]
    """
    return scipy.signal.lfilter([1], [1, float(-discount)], x[::-1], axis=0)[::-1]


class Actor(nn.Module):

    def _distribution(self, obs):
        raise NotImplementedError

    def _log_prob_from_distribution(self, pi, act):
        raise NotImplementedError

    def forward(self, obs, act=None):
        # Produce action distributions for given observations, and 
        # optionally compute the log likelihood of given actions under
        # those distributions.
        pi = self._distribution(obs)
        logp_a = None
        if act is not None:
            logp_a = self._log_prob_from_distribution(pi, act)
        return pi, logp_a


class MLPCategoricalActor(Actor):
    
    def __init__(self, obs_dim, act_dim, hidden_sizes, activation):
        super().__init__()
        self.logits_net = mlp([obs_dim] + list(hidden_sizes) + [act_dim], activation)

    def _distribution(self, obs):
        logits = self.logits_net(obs)
        return Categorical(logits=logits)

    def _log_prob_from_distribution(self, pi, act):
        return pi.log_prob(act)


class MLPGaussianActor(Actor):

    def __init__(self, obs_dim, act_dim, hidden_sizes, activation):
        super().__init__()
        log_std = -0.5 * np.ones(act_dim, dtype=np.float32)
        self.log_std = torch.nn.Parameter(torch.as_tensor(log_std))
        self.mu_net = mlp([obs_dim] + list(hidden_sizes) + [act_dim], activation)

    def _distribution(self, obs):
        mu = self.mu_net(obs)
        std = torch.exp(self.log_std)
        return Normal(mu, std)

    def _log_prob_from_distribution(self, pi, act):
        return pi.log_prob(act).sum(axis=-1)    # Last axis sum needed for Torch Normal distribution


class MLPCritic(nn.Module):

    def __init__(self, obs_dim, hidden_sizes, activation):
        super().__init__()
        self.v_net = mlp([obs_dim] + list(hidden_sizes) + [1], activation)

    def forward(self, obs):
        return torch.squeeze(self.v_net(obs), -1) # Critical to ensure v has right shape.



class MLPActorCritic(nn.Module):


    def __init__(self, observation_space, action_space, 
                 hidden_sizes=(64,64), activation=nn.Tanh):
        super().__init__()

        obs_dim = observation_space.shape[0]

        # policy builder depends on action space
        if isinstance(action_space, Box):
            self.pi = MLPGaussianActor(obs_dim, action_space.shape[0], hidden_sizes, activation)
        elif isinstance(action_space, Discrete):
            self.pi = MLPCategoricalActor(obs_dim, action_space.n, hidden_sizes, activation)

        # build value function
        self.v  = MLPCritic(obs_dim, hidden_sizes, activation)

    def step(self, obs):
        with torch.no_grad():
            pi = self.pi._distribution(obs)
            a = pi.sample()
            logp_a = self.pi._log_prob_from_distribution(pi, a)
            v = self.v(obs)
        return a.numpy(), v.numpy(), logp_a.numpy()

    def act(self, obs):
        return self.step(obs)[0]

class PPOBuffer:
    """
    A buffer for storing trajectories experienced by a PPO agent interacting
    with the environment, and using Generalized Advantage Estimation (GAE-Lambda)
    for calculating the advantages of state-action pairs.
    """

    def __init__(self, obs_dim, act_dim, size, gamma=0.99, lam=0.95):
        self.obs_buf = np.zeros(combined_shape(size, obs_dim), dtype=np.float32)
        self.act_buf = np.zeros(combined_shape(size, act_dim), dtype=np.float32)
        self.adv_buf = np.zeros(size, dtype=np.float32)
        self.rew_buf = np.zeros(size, dtype=np.float32)
        self.ret_buf = np.zeros(size, dtype=np.float32)
        self.val_buf = np.zeros(size, dtype=np.float32)
        self.logp_buf = np.zeros(size, dtype=np.float32)
        self.gamma, self.lam = gamma, lam
        self.ptr, self.path_start_idx, self.max_size = 0, 0, size

    def store(self, obs, act, rew, val, logp):
        """
        Append one timestep of agent-environment interaction to the buffer.
        """
        assert self.ptr < self.max_size     # buffer has to have room so you can store
        self.obs_buf[self.ptr] = obs
        self.act_buf[self.ptr] = act
        self.rew_buf[self.ptr] = rew
        self.val_buf[self.ptr] = val
        self.logp_buf[self.ptr] = logp
        self.ptr += 1

    def finish_path(self, last_val=0):
        """
        Call this at the end of a trajectory, or when one gets cut off
        by an epoch ending. This looks back in the buffer to where the
        trajectory started, and uses rewards and value estimates from
        the whole trajectory to compute advantage estimates with GAE-Lambda,
        as well as compute the rewards-to-go for each state, to use as
        the targets for the value function.
        The "last_val" argument should be 0 if the trajectory ended
        because the agent reached a terminal state (died), and otherwise
        should be V(s_T), the value function estimated for the last state.
        This allows us to bootstrap the reward-to-go calculation to account
        for timesteps beyond the arbitrary episode horizon (or epoch cutoff).
        """

        path_slice = slice(self.path_start_idx, self.ptr)
        rews = np.append(self.rew_buf[path_slice], last_val)
        vals = np.append(self.val_buf[path_slice], last_val)
        
        # the next two lines implement GAE-Lambda advantage calculation
        deltas = rews[:-1] + self.gamma * vals[1:] - vals[:-1]
        self.adv_buf[path_slice] = discount_cumsum(deltas, self.gamma * self.lam)
        
        # the next line computes rewards-to-go, to be targets for the value function
        self.ret_buf[path_slice] = discount_cumsum(rews, self.gamma)[:-1]
        
        self.path_start_idx = self.ptr

    def get(self):
        """
        Call this at the end of an epoch to get all of the data from
        the buffer, with advantages appropriately normalized (shifted to have
        mean zero and std one). Also, resets some pointers in the buffer.
        """
        assert self.ptr == self.max_size    # buffer has to be full before you can get
        self.ptr, self.path_start_idx = 0, 0
        # the next two lines implement the advantage normalization trick
        self.adv_buf = (self.adv_buf - np.mean(self.adv_buf)) / np.std(self.adv_buf)
        data = dict(obs=self.obs_buf, act=self.act_buf, ret=self.ret_buf,
                    adv=self.adv_buf, logp=self.logp_buf)
        return {k: torch.as_tensor(v, dtype=torch.float32) for k,v in data.items()}

def ppo(env_fn, actor_critic=MLPActorCritic, ac_kwargs=dict(), seed=0, 
        steps_per_epoch=4000, epochs=50, gamma=0.99, clip_ratio=0.2, pi_lr=3e-4,
        vf_lr=1e-3, train_pi_iters=80, train_v_iters=80, lam=0.97, max_ep_len=1000,
        target_kl=0.01, save_freq=10):
    """
    Proximal Policy Optimization (by clipping), 
    with early stopping based on approximate KL
    Args:
        env_fn : A function which creates a copy of the environment.
            The environment must satisfy the OpenAI Gym API.
        actor_critic: The constructor method for a PyTorch Module with a 
            ``step`` method, an ``act`` method, a ``pi`` module, and a ``v`` 
            module. The ``step`` method should accept a batch of observations 
            and return:
            ===========  ================  ======================================
            Symbol       Shape             Description
            ===========  ================  ======================================
            ``a``        (batch, act_dim)  | Numpy array of actions for each 
                                           | observation.
            ``v``        (batch,)          | Numpy array of value estimates
                                           | for the provided observations.
            ``logp_a``   (batch,)          | Numpy array of log probs for the
                                           | actions in ``a``.
            ===========  ================  ======================================
            The ``act`` method behaves the same as ``step`` but only returns ``a``.
            The ``pi`` module's forward call should accept a batch of 
            observations and optionally a batch of actions, and return:
            ===========  ================  ======================================
            Symbol       Shape             Description
            ===========  ================  ======================================
            ``pi``       N/A               | Torch Distribution object, containing
                                           | a batch of distributions describing
                                           | the policy for the provided observations.
            ``logp_a``   (batch,)          | Optional (only returned if batch of
                                           | actions is given). Tensor containing 
                                           | the log probability, according to 
                                           | the policy, of the provided actions.
                                           | If actions not given, will contain
                                           | ``None``.
            ===========  ================  ======================================
            The ``v`` module's forward call should accept a batch of observations
            and return:
            ===========  ================  ======================================
            Symbol       Shape             Description
            ===========  ================  ======================================
            ``v``        (batch,)          | Tensor containing the value estimates
                                           | for the provided observations. (Critical: 
                                           | make sure to flatten this!)
            ===========  ================  ======================================
        ac_kwargs (dict): Any kwargs appropriate for the ActorCritic object 
            you provided to PPO.
        seed (int): Seed for random number generators.
        steps_per_epoch (int): Number of steps of interaction (state-action pairs) 
            for the agent and the environment in each epoch.
        epochs (int): Number of epochs of interaction (equivalent to
            number of policy updates) to perform.
        gamma (float): Discount factor. (Always between 0 and 1.)
        clip_ratio (float): Hyperparameter for clipping in the policy objective.
            Roughly: how far can the new policy go from the old policy while 
            still profiting (improving the objective function)? The new policy 
            can still go farther than the clip_ratio says, but it doesn't help
            on the objective anymore. (Usually small, 0.1 to 0.3.) Typically
            denoted by :math:`\epsilon`. 
        pi_lr (float): Learning rate for policy optimizer.
        vf_lr (float): Learning rate for value function optimizer.
        train_pi_iters (int): Maximum number of gradient descent steps to take 
            on policy loss per epoch. (Early stopping may cause optimizer
            to take fewer than this.)
        train_v_iters (int): Number of gradient descent steps to take on 
            value function per epoch.
        lam (float): Lambda for GAE-Lambda. (Always between 0 and 1,
            close to 1.)
        max_ep_len (int): Maximum length of trajectory / episode / rollout.
        target_kl (float): Roughly what KL divergence we think is appropriate
            between new and old policies after an update. This will get used 
            for early stopping. (Usually small, 0.01 or 0.05.)
        logger_kwargs (dict): Keyword args for EpochLogger.
        save_freq (int): How often (in terms of gap between epochs) to save
            the current policy and value function.
    """

    # Random seed
    torch.manual_seed(seed)
    np.random.seed(seed)

    # Instantiate environment
    env = env_fn()
    obs_dim = env.observation_space.shape
    act_dim = env.action_space.shape

    # Create actor-critic module
    ac = actor_critic(env.observation_space, env.action_space, **ac_kwargs)

    # Count variables
    var_counts = tuple(count_vars(module) for module in [ac.pi, ac.v])
    print('\nNumber of parameters: \t pi: %d, \t v: %d\n'%var_counts)

    # Set up experience buffer
    buf = PPOBuffer(obs_dim, act_dim, int(steps_per_epoch), gamma, lam)

    # Set up function for computing PPO policy loss
    def compute_loss_pi(data):
        obs, act, adv, logp_old = data['obs'], data['act'], data['adv'], data['logp']

        # Policy loss
        pi, logp = ac.pi(obs, act)
        ratio = torch.exp(logp - logp_old)
        clip_adv = torch.clamp(ratio, 1-clip_ratio, 1+clip_ratio) * adv
        loss_pi = -(torch.min(ratio * adv, clip_adv)).mean()

        # Useful extra info
        approx_kl = (logp_old - logp).mean().item()
        ent = pi.entropy().mean().item()
        clipped = ratio.gt(1+clip_ratio) | ratio.lt(1-clip_ratio)
        clipfrac = torch.as_tensor(clipped, dtype=torch.float32).mean().item()
        pi_info = dict(kl=approx_kl, ent=ent, cf=clipfrac)

        return loss_pi, pi_info

    # Set up function for computing value loss
    def compute_loss_v(data):
        obs, ret = data['obs'], data['ret']
        return ((ac.v(obs) - ret)**2).mean()

    # Set up optimizers for policy and value function
    pi_optimizer = Adam(ac.pi.parameters(), lr=pi_lr)
    vf_optimizer = Adam(ac.v.parameters(), lr=vf_lr)

    def update():
        data = buf.get()

        pi_l_old, pi_info_old = compute_loss_pi(data)
        pi_l_old = pi_l_old.item()
        v_l_old = compute_loss_v(data).item()

        # Train policy with multiple steps of gradient descent
        for i in range(train_pi_iters):
            pi_optimizer.zero_grad()
            loss_pi, pi_info = compute_loss_pi(data)
            
            if pi_info['kl'] > 1.5 * target_kl:
                print('Early stopping at step %d due to reaching max kl.'%i)
                break
            loss_pi.backward()
            pi_optimizer.step()

        # Value function learning
        for i in range(train_v_iters):
            vf_optimizer.zero_grad()
            loss_v = compute_loss_v(data)
            loss_v.backward()
            vf_optimizer.step()

        # Log changes from update
        print("DeltaLossPi={:.2f}, DeltaLossV={:.2f}".format(loss_pi.item() - pi_l_old, \
                                                             loss_v.item() - v_l_old))

    # Prepare for interaction with environment
    start_time = time.time()
    o, ep_ret, ep_len = env.reset(), 0, 0
    
    average_ret = []
    # Main loop: collect experience in env and update/log each epoch
    for epoch in range(epochs):
        check_point_ret = []
        for t in range(steps_per_epoch):
            a, v, logp = ac.step(torch.as_tensor(o, dtype=torch.float32))

            next_o, r, d, _ = env.step(a)
            ep_ret += r
            ep_len += 1

            # save and log
            buf.store(o, a, r, v, logp)
            
            # Update obs (critical!)
            o = next_o

            timeout = ep_len == max_ep_len
            terminal = d or timeout
            epoch_ended = t==steps_per_epoch-1

            if terminal or epoch_ended:
                if epoch_ended and not(terminal):
                    print('Warning: trajectory cut off by epoch at %d steps.'%ep_len, flush=True)
                # if trajectory didn't reach terminal state, bootstrap value target
                if timeout or epoch_ended:
                    _, v, _ = ac.step(torch.as_tensor(o, dtype=torch.float32))
                else:
                    v = 0
                buf.finish_path(v)
                if terminal:
                    # only save EpRet / EpLen if trajectory finished
                    print("Episodic Ret={:.2f}, Episodic Len={:.2f}".format(ep_ret, ep_len))
                    check_point_ret.append(ep_ret)
                o, ep_ret, ep_len = env.reset(), 0, 0

        
        print("Epoch: {}".format(epoch))
        # record improvement
        average_ret.append(np.mean(check_point_ret))

        # Perform PPO update!
        update()
        
    return average_ret

<>:5: DeprecationWarning: invalid escape sequence \e

import argparse
parser = argparse.ArgumentParser()
parser.add_argument('--env', type=str, default="BipedalWalker-v3")
# To use to the hardcore environment, you need to specify the hardcore=True argument
# env = gym.make("BipedalWalker-v3", hardcore=True)
parser.add_argument('--hid', type=int, default=64)
parser.add_argument('--l', type=int, default=2)
parser.add_argument('--gamma', type=float, default=0.99)
parser.add_argument('--seed', '-s', type=int, default=0)
parser.add_argument('--steps', type=int, default=4000)
parser.add_argument('--epochs', type=int, default=50)
args, unknown = parser.parse_known_args()


average_ret = ppo(lambda : gym.make(args.env), actor_critic=MLPActorCritic,
    ac_kwargs=dict(hidden_sizes=[args.hid]*args.l), gamma=args.gamma, 
    seed=args.seed, steps_per_epoch=args.steps, epochs=args.epochs,)

Number of parameters: 	 pi: 6024, 	 v: 5825

Episodic Ret=-49.82, Episodic Len=1000.00
Episodic Ret=-49.46, Episodic Len=1000.00
Episodic Ret=-108.25, Episodic Len=74.00
Episodic Ret=-97.25, Episodic Len=88.00
Episodic Ret=-122.20, Episodic Len=127.00
Episodic Ret=-118.35, Episodic Len=60.00
Episodic Ret=-116.01, Episodic Len=85.00
Episodic Ret=-112.22, Episodic Len=70.00
Episodic Ret=-46.72, Episodic Len=1000.00
Episodic Ret=-102.36, Episodic Len=54.00
Episodic Ret=-120.68, Episodic Len=75.00
Warning: trajectory cut off by epoch at 367 steps.
Epoch: 0
DeltaLossPi=-0.01, DeltaLossV=-193.73
Episodic Ret=-117.93, Episodic Len=68.00
Episodic Ret=-118.57, Episodic Len=71.00
Episodic Ret=-101.59, Episodic Len=74.00
Episodic Ret=-47.25, Episodic Len=1000.00
Episodic Ret=-46.59, Episodic Len=1000.00
Episodic Ret=-108.04, Episodic Len=45.00
Episodic Ret=-53.12, Episodic Len=1000.00
Episodic Ret=-118.99, Episodic Len=135.00
Warning: trajectory cut off by epoch at 607 steps.
Epoch: 1
DeltaLossPi=-0.02, DeltaLossV=-41.39
Episodic Ret=-104.48, Episodic Len=80.00
Episodic Ret=-113.39, Episodic Len=60.00
Episodic Ret=-48.46, Episodic Len=1000.00
Episodic Ret=-109.15, Episodic Len=131.00
Episodic Ret=-50.44, Episodic Len=1000.00
Episodic Ret=-101.05, Episodic Len=112.00
Episodic Ret=-53.58, Episodic Len=1000.00
Episodic Ret=-108.71, Episodic Len=50.00
Warning: trajectory cut off by epoch at 567 steps.
Epoch: 2
DeltaLossPi=-0.02, DeltaLossV=-56.66
Episodic Ret=-52.94, Episodic Len=1000.00
Episodic Ret=-98.16, Episodic Len=102.00
Episodic Ret=-51.59, Episodic Len=1000.00
Episodic Ret=-102.22, Episodic Len=73.00
Episodic Ret=-106.17, Episodic Len=83.00
Episodic Ret=-51.13, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 742 steps.
Epoch: 3
DeltaLossPi=-0.01, DeltaLossV=-24.90
Episodic Ret=-48.40, Episodic Len=1000.00
Episodic Ret=-101.94, Episodic Len=86.00
Episodic Ret=-50.62, Episodic Len=1000.00
Episodic Ret=-51.49, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 914 steps.
Epoch: 4
DeltaLossPi=-0.01, DeltaLossV=-5.88
Episodic Ret=-100.28, Episodic Len=70.00
Episodic Ret=-102.39, Episodic Len=60.00
Episodic Ret=-51.18, Episodic Len=1000.00
Episodic Ret=-55.31, Episodic Len=1000.00
Episodic Ret=-101.26, Episodic Len=53.00
Episodic Ret=-98.00, Episodic Len=77.00
Episodic Ret=-51.36, Episodic Len=1000.00
Episodic Ret=-104.15, Episodic Len=75.00
Warning: trajectory cut off by epoch at 665 steps.
Epoch: 5
DeltaLossPi=-0.02, DeltaLossV=-48.31
Episodic Ret=-54.39, Episodic Len=1000.00
Episodic Ret=-117.54, Episodic Len=83.00
Episodic Ret=-50.19, Episodic Len=1000.00
Episodic Ret=-100.69, Episodic Len=83.00
Episodic Ret=-99.49, Episodic Len=114.00
Episodic Ret=-55.70, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 720 steps.
Epoch: 6
DeltaLossPi=-0.02, DeltaLossV=-40.69
Episodic Ret=-58.54, Episodic Len=1000.00
Episodic Ret=-57.52, Episodic Len=1000.00
Episodic Ret=-58.34, Episodic Len=1000.00
Episodic Ret=-52.94, Episodic Len=1000.00
Epoch: 7
DeltaLossPi=-0.02, DeltaLossV=-6.33
Episodic Ret=-50.19, Episodic Len=1000.00
Episodic Ret=-49.88, Episodic Len=1000.00
Episodic Ret=-56.56, Episodic Len=1000.00
Episodic Ret=-51.16, Episodic Len=1000.00
Epoch: 8
Early stopping at step 5 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-1.94
Episodic Ret=-57.32, Episodic Len=1000.00
Episodic Ret=-116.96, Episodic Len=72.00
Episodic Ret=-106.12, Episodic Len=76.00
Episodic Ret=-48.67, Episodic Len=1000.00
Episodic Ret=-45.16, Episodic Len=1000.00
Episodic Ret=-119.71, Episodic Len=101.00
Warning: trajectory cut off by epoch at 751 steps.
Epoch: 9
Early stopping at step 36 due to reaching max kl.
DeltaLossPi=-0.02, DeltaLossV=-132.63
Episodic Ret=-44.97, Episodic Len=1000.00
Episodic Ret=-114.19, Episodic Len=69.00
Episodic Ret=-48.86, Episodic Len=1000.00
Episodic Ret=-45.78, Episodic Len=1000.00
Episodic Ret=-105.31, Episodic Len=105.00
Episodic Ret=-97.61, Episodic Len=108.00
Episodic Ret=-108.80, Episodic Len=54.00
Warning: trajectory cut off by epoch at 664 steps.
Epoch: 10
Early stopping at step 7 due to reaching max kl.
DeltaLossPi=-0.01, DeltaLossV=-82.88
Episodic Ret=-55.30, Episodic Len=1000.00
Episodic Ret=-44.32, Episodic Len=1000.00
Episodic Ret=-42.77, Episodic Len=1000.00
Episodic Ret=-38.79, Episodic Len=1000.00
Epoch: 11
Early stopping at step 17 due to reaching max kl.
DeltaLossPi=-0.01, DeltaLossV=-15.30
Episodic Ret=-50.35, Episodic Len=1000.00
Episodic Ret=-43.89, Episodic Len=1000.00
Episodic Ret=-43.60, Episodic Len=1000.00
Episodic Ret=-43.42, Episodic Len=1000.00
Epoch: 12
DeltaLossPi=-0.01, DeltaLossV=-0.56
Episodic Ret=-51.58, Episodic Len=1000.00
Episodic Ret=-45.65, Episodic Len=1000.00
Episodic Ret=-47.01, Episodic Len=1000.00
Episodic Ret=-47.63, Episodic Len=1000.00
Epoch: 13
DeltaLossPi=-0.01, DeltaLossV=-0.06
Episodic Ret=-48.77, Episodic Len=1000.00
Episodic Ret=-48.36, Episodic Len=1000.00
Episodic Ret=-43.41, Episodic Len=1000.00
Episodic Ret=-43.06, Episodic Len=1000.00
Epoch: 14
DeltaLossPi=-0.01, DeltaLossV=-0.10
Episodic Ret=-44.81, Episodic Len=1000.00
Episodic Ret=-46.16, Episodic Len=1000.00
Episodic Ret=-42.71, Episodic Len=1000.00
Episodic Ret=-40.21, Episodic Len=1000.00
Epoch: 15
DeltaLossPi=-0.02, DeltaLossV=-0.09
Episodic Ret=-110.32, Episodic Len=50.00
Episodic Ret=-41.16, Episodic Len=1000.00
Episodic Ret=-42.81, Episodic Len=1000.00
Episodic Ret=-34.33, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 950 steps.
Epoch: 16
Early stopping at step 76 due to reaching max kl.
DeltaLossPi=-0.01, DeltaLossV=-24.37
Episodic Ret=-43.80, Episodic Len=1000.00
Episodic Ret=-39.41, Episodic Len=1000.00
Episodic Ret=-116.43, Episodic Len=67.00
Episodic Ret=-39.31, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 933 steps.
Epoch: 17
DeltaLossPi=-0.01, DeltaLossV=-36.21
Episodic Ret=-110.64, Episodic Len=86.00
Episodic Ret=-108.98, Episodic Len=67.00
Episodic Ret=-39.49, Episodic Len=1000.00
Episodic Ret=-43.95, Episodic Len=1000.00
Episodic Ret=-28.40, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 847 steps.
Epoch: 18
DeltaLossPi=-0.02, DeltaLossV=-25.09
Episodic Ret=-43.93, Episodic Len=1000.00
Episodic Ret=-118.91, Episodic Len=61.00
Episodic Ret=-43.10, Episodic Len=1000.00
Episodic Ret=-40.76, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 939 steps.
Epoch: 19
DeltaLossPi=-0.01, DeltaLossV=-13.67
Episodic Ret=-44.76, Episodic Len=1000.00
Episodic Ret=-47.49, Episodic Len=1000.00
Episodic Ret=-39.61, Episodic Len=1000.00
Episodic Ret=-43.12, Episodic Len=1000.00
Epoch: 20
DeltaLossPi=-0.01, DeltaLossV=-5.71
Episodic Ret=-38.43, Episodic Len=1000.00
Episodic Ret=-43.32, Episodic Len=1000.00
Episodic Ret=-46.32, Episodic Len=1000.00
Episodic Ret=-41.36, Episodic Len=1000.00
Epoch: 21
Early stopping at step 6 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-3.59
Episodic Ret=-35.10, Episodic Len=1000.00
Episodic Ret=-42.23, Episodic Len=1000.00
Episodic Ret=-35.52, Episodic Len=1000.00
Episodic Ret=-29.74, Episodic Len=1000.00
Epoch: 22
DeltaLossPi=-0.02, DeltaLossV=-0.52
Episodic Ret=-37.97, Episodic Len=1000.00
Episodic Ret=-39.05, Episodic Len=1000.00
Episodic Ret=-33.42, Episodic Len=1000.00
Episodic Ret=-36.29, Episodic Len=1000.00
Epoch: 23
DeltaLossPi=-0.02, DeltaLossV=-0.04
Episodic Ret=-39.74, Episodic Len=1000.00
Episodic Ret=-33.37, Episodic Len=1000.00
Episodic Ret=-38.34, Episodic Len=1000.00
Episodic Ret=-31.71, Episodic Len=1000.00
Epoch: 24
Early stopping at step 4 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-0.05
Episodic Ret=-32.43, Episodic Len=1000.00
Episodic Ret=-34.62, Episodic Len=1000.00
Episodic Ret=-35.03, Episodic Len=1000.00
Episodic Ret=-31.66, Episodic Len=1000.00
Epoch: 25
Early stopping at step 3 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-0.03
Episodic Ret=-30.58, Episodic Len=1000.00
Episodic Ret=-32.26, Episodic Len=1000.00
Episodic Ret=-33.94, Episodic Len=1000.00
Episodic Ret=-30.55, Episodic Len=1000.00
Epoch: 26
DeltaLossPi=-0.01, DeltaLossV=-0.10
Episodic Ret=-36.84, Episodic Len=1000.00
Episodic Ret=-28.47, Episodic Len=1000.00
Episodic Ret=-33.80, Episodic Len=1000.00
Episodic Ret=-26.20, Episodic Len=1000.00
Epoch: 27
DeltaLossPi=-0.02, DeltaLossV=-0.07
Episodic Ret=-30.88, Episodic Len=1000.00
Episodic Ret=-29.36, Episodic Len=1000.00
Episodic Ret=-24.18, Episodic Len=1000.00
Episodic Ret=-29.44, Episodic Len=1000.00
Epoch: 28
DeltaLossPi=-0.02, DeltaLossV=-0.04
Episodic Ret=-24.69, Episodic Len=1000.00
Episodic Ret=-31.80, Episodic Len=1000.00
Episodic Ret=-19.87, Episodic Len=1000.00
Episodic Ret=-31.40, Episodic Len=1000.00
Epoch: 29
DeltaLossPi=-0.02, DeltaLossV=-0.12
Episodic Ret=-13.44, Episodic Len=1000.00
Episodic Ret=-17.44, Episodic Len=1000.00
Episodic Ret=-31.43, Episodic Len=1000.00
Episodic Ret=-28.74, Episodic Len=1000.00
Epoch: 30
DeltaLossPi=-0.02, DeltaLossV=-0.20
Episodic Ret=-19.28, Episodic Len=1000.00
Episodic Ret=-23.64, Episodic Len=1000.00
Episodic Ret=-12.91, Episodic Len=1000.00
Episodic Ret=-18.36, Episodic Len=1000.00
Epoch: 31
DeltaLossPi=-0.02, DeltaLossV=-0.19
Episodic Ret=-14.75, Episodic Len=1000.00
Episodic Ret=-22.35, Episodic Len=1000.00
Episodic Ret=-23.69, Episodic Len=1000.00
Episodic Ret=-10.84, Episodic Len=1000.00
Epoch: 32
DeltaLossPi=-0.02, DeltaLossV=-0.36
Episodic Ret=-20.05, Episodic Len=1000.00
Episodic Ret=-9.15, Episodic Len=1000.00
Episodic Ret=-13.02, Episodic Len=1000.00
Episodic Ret=-15.69, Episodic Len=1000.00
Epoch: 33
DeltaLossPi=-0.02, DeltaLossV=-0.11
Episodic Ret=-10.58, Episodic Len=1000.00
Episodic Ret=-8.50, Episodic Len=1000.00
Episodic Ret=-2.78, Episodic Len=1000.00
Episodic Ret=-17.64, Episodic Len=1000.00
Epoch: 34
DeltaLossPi=-0.02, DeltaLossV=-0.51
Episodic Ret=-109.78, Episodic Len=59.00
Episodic Ret=-3.25, Episodic Len=1000.00
Episodic Ret=-2.39, Episodic Len=1000.00
Episodic Ret=-111.19, Episodic Len=55.00
Episodic Ret=-12.19, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 886 steps.
Epoch: 35
Early stopping at step 5 due to reaching max kl.
DeltaLossPi=-0.01, DeltaLossV=-54.64
Episodic Ret=-12.67, Episodic Len=1000.00
Episodic Ret=1.38, Episodic Len=1000.00
Episodic Ret=-107.08, Episodic Len=693.00
Episodic Ret=-4.18, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 307 steps.
Epoch: 36
DeltaLossPi=-0.02, DeltaLossV=-20.00
Episodic Ret=-7.88, Episodic Len=1000.00
Episodic Ret=-2.70, Episodic Len=1000.00
Episodic Ret=-2.82, Episodic Len=1000.00
Episodic Ret=-13.12, Episodic Len=1000.00
Epoch: 37
Early stopping at step 4 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-3.47
Episodic Ret=-9.17, Episodic Len=1000.00
Episodic Ret=-6.67, Episodic Len=1000.00
Episodic Ret=-5.34, Episodic Len=1000.00
Episodic Ret=2.00, Episodic Len=1000.00
Epoch: 38
DeltaLossPi=-0.02, DeltaLossV=-0.20
Episodic Ret=-8.06, Episodic Len=1000.00
Episodic Ret=-2.59, Episodic Len=1000.00
Episodic Ret=9.68, Episodic Len=1000.00
Episodic Ret=-9.98, Episodic Len=1000.00
Epoch: 39
DeltaLossPi=-0.01, DeltaLossV=-0.15
Episodic Ret=-3.68, Episodic Len=1000.00
Episodic Ret=1.29, Episodic Len=1000.00
Episodic Ret=0.01, Episodic Len=1000.00
Episodic Ret=-4.43, Episodic Len=1000.00
Epoch: 40
DeltaLossPi=-0.01, DeltaLossV=-0.15
Episodic Ret=1.65, Episodic Len=1000.00
Episodic Ret=2.54, Episodic Len=1000.00
Episodic Ret=7.52, Episodic Len=1000.00
Episodic Ret=-99.74, Episodic Len=79.00
Warning: trajectory cut off by epoch at 921 steps.
Epoch: 41
DeltaLossPi=-0.02, DeltaLossV=-34.52
Episodic Ret=3.68, Episodic Len=1000.00
Episodic Ret=5.80, Episodic Len=1000.00
Episodic Ret=1.26, Episodic Len=1000.00
Episodic Ret=0.08, Episodic Len=1000.00
Epoch: 42
Early stopping at step 4 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-0.48
Episodic Ret=2.63, Episodic Len=1000.00
Episodic Ret=19.94, Episodic Len=1000.00
Episodic Ret=12.05, Episodic Len=1000.00
Episodic Ret=1.10, Episodic Len=1000.00
Epoch: 43
DeltaLossPi=-0.01, DeltaLossV=-0.78
Episodic Ret=-4.68, Episodic Len=1000.00
Episodic Ret=5.37, Episodic Len=1000.00
Episodic Ret=13.18, Episodic Len=1000.00
Episodic Ret=-117.46, Episodic Len=85.00
Warning: trajectory cut off by epoch at 915 steps.
Epoch: 44
Early stopping at step 13 due to reaching max kl.
DeltaLossPi=-0.01, DeltaLossV=-4.11
Episodic Ret=-118.21, Episodic Len=97.00
Episodic Ret=-4.89, Episodic Len=1000.00
Episodic Ret=13.13, Episodic Len=1000.00
Episodic Ret=4.10, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 903 steps.
Epoch: 45
Early stopping at step 5 due to reaching max kl.
DeltaLossPi=-0.00, DeltaLossV=-6.07
Episodic Ret=9.50, Episodic Len=1000.00
Episodic Ret=-110.43, Episodic Len=56.00
Episodic Ret=20.94, Episodic Len=1000.00
Episodic Ret=12.17, Episodic Len=1000.00
Warning: trajectory cut off by epoch at 944 steps.
Epoch: 46
DeltaLossPi=-0.02, DeltaLossV=-8.06
Episodic Ret=0.36, Episodic Len=1000.00
Episodic Ret=5.83, Episodic Len=1000.00
Episodic Ret=10.09, Episodic Len=1000.00
Episodic Ret=-2.32, Episodic Len=1000.00
Epoch: 47
DeltaLossPi=-0.02, DeltaLossV=-0.59
Episodic Ret=23.15, Episodic Len=1000.00
Episodic Ret=12.53, Episodic Len=1000.00
Episodic Ret=39.45, Episodic Len=1000.00
Episodic Ret=6.06, Episodic Len=1000.00
Epoch: 48
DeltaLossPi=-0.01, DeltaLossV=-1.86
Episodic Ret=27.47, Episodic Len=1000.00
Episodic Ret=36.24, Episodic Len=1000.00
Episodic Ret=17.64, Episodic Len=1000.00
Episodic Ret=-98.18, Episodic Len=135.00
Warning: trajectory cut off by epoch at 865 steps.
Epoch: 49
Early stopping at step 15 due to reaching max kl.
DeltaLossPi=-0.01, DeltaLossV=-45.70

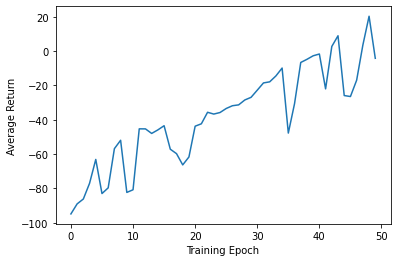
import matplotlib.pyplot as plt

plt.figure()
plt.plot(average_ret)
plt.xlabel('Training Epoch')
plt.ylabel('Average Return')
plt.show()